Preliminary version 30 November 2005
Nir Dagan, Academic College of Judea and Samaria, Ariel. <nir@nirdagan.com>
Yossi Tobol, Bar Ilan University, Ramat-Gan, and Academic College of Judea and Samaria, Ariel.
We analyze the interaction between the tax authority, tax payers, and potential informants in a game theoretic framework. The tax authority gives monetary incentives to informants, and conducts random tax audits. The probability of a tax payer being audited depends on whether the tax authority received a tip about him from an informant or not. In subgame perfect equilibrium tax payers are divided into (at most) two groups. Those with income up to a certain level evade a small amount of taxes to assure that potential informants do not have sufficient incentives to report, and those with high incomes choose to declare zero income knowing that they will be reported by informants. The tax authority chooses the probabilities of the two types of audits, under a budget constraint. In many cases the probabilities are chosen in a way that no informant actually reported, and in some cases the tax authority does not conduct any audits.
This article analyses interaction between tax payers, informants, and the tax authority, in a game theoretic framework. Our contribution may be viewed as either extending game theoretic models that consider only tax payers and the tax authority, in a game theoretic framework, or as extending the study of the role of informants to a more comprehensive framework than analyzed before.
The basic papers on tax evasion ask how a potential tax evader would report to the tax authority as a consequence of having solved an optimization problem. They further inquire how the level of reporting would change as a result of higher/lower tax rates. (See Allingham & Sandmo 1972; Srinivasan 1973 for more details).
The first paper on tax evasion analyzed in a game-theoretical method is Greenberg (1984). He analyzes interaction between a tax authority, which could classify a potential tax evader, and the tax evader. Of the three categories determined by the tax authority, the first is sampled randomly, and the so is the second, albeit at a lower probability than the first. The third category is examined consistently, that is, definitely. Thus, the tax authority investigates a potential evader. If she is caught, she is moved to the third category at the next tax period. Otherwise, she is moved to the first. Greenberg shows the in an equilibrium in which all players have all the knowledge and information available, a certain proportion of potential tax evaders will not be examined at all, while the others will always be examined.
Graetz, Reinganum and Wilde (1986a) studies a a normal form game between the tax authority and a tax payer. The paper examines each player�s behavior vis-�-vis the other. The potential evader decides whether to evade or not, and the tax authority decides to audit or not. They show when we can expect a pure versus mixed equilibrium. It focuses on the mixed variety, meaning that the potential evader evades at a positive probability, while the tax authority investigates at a positive probability.
Graetz, Reinganum and Wilde (1986b) studies an extensive form game. In the first phase, the potential evader reports his taxable income to the tax authority, and at the second, the tax authority uses that information to decide whether to investigate or not. Graetz et al. show that in equilibrium, the investigation policy is to focus on the lower reported incomes. This equilibrium result is interesting: despite the fact that the tax authority investigates the lower reported incomes, those with higher incomes report lower incomes than those with truly lower incomes. These results are applicable to linear taxation. (For more details and similar games, see Scotchmer 1987; Mookherjee & Png 1989; Sanchez & Sobel 1993 � all using the �principal agent� method).
Models of a different kind assume that there are two types of individuals: those who would never evade taxes � honest players � and those who may consider whether to evade based on incentives, or strategic players. In such a model, the resulting equilibrium is different, since the tax authority does not differentiate between player types before an audit, as opposed to the previous models where all individuals behave strategically. This approach is based on sociological and psychological literature (e.g., Cowell 1990; Erard & Feinstein 1994). Some models have combined tax evasion and corruption, such that the evader bribes the tax authority�s representative. Thus, in effect, the evader and the corrupt representative agree on a deal detrimental to the tax authority (Hindriks, Keen & Muthoo 1999; Marjit, Mukherjee & Mukherjee 2000; Saha 2003; Marjit, Mukherjee & Mukherjee 2003).
Despite the extensive literature on the subject, not a single paper has hitherto discussed tax evasion informants, apart from one (Yaniv 2001). Yaniv describes a common issue between the tax authority and a potential informant trying to decide whether to inform on a �colleague�, for example, his self-employed boss. One can also suggest the situation of a divorced couple, in which the woman considers informing on her husband as a form of revenge (see Elster 1988). The potential informant is can have several motives, such as strong integrity, loyalty to the rule of law, financial reward or revenge against the evader. The last two motives are of course the strongest, and we know for a fact that most such reports result from a personal conflict between the informant and the potential evader. In other cases, people inform for money (Yaniv 2001). In addition, Yaniv�s paper considers the tax authority�s side: it has to decide on the optimal reward for the informant and what effort it should make to have a certain report lead to conviction and punishment. Last but not least, the informant should decide whether to inform or not.
The rest of article is organized as follows:.....
There is a flat income tax of θ, 0<θ<1. Tax payers declare their incomes to the tax authority, but may evade taxes by under reporting their true incomes. In order to enforce the tax law, the tax authority may audit tax payers randomly as well as using informants. Denote by pr the probability that the tax authority will conduct a random audit, among those tax payers that no informant reported on, and by pi is the probability that the tax authority will conduct an audit due to an informant's report.
The probability that a tax payer will be convicted of tax evasion, given that an audit took place is β, 0<β≤1. We assume that once convicted, the total under reporting is discovered. Thus we implicitly assume that the taxation authority cannot conduct different kinds of audits (possibly with different costs), and that the success rate is not a function of the under reported income. Once a tax payer is convicted of tax evasion, he pays the evaded tax times π, where π>1.
The tax authority motivates informants by paying them a bounty whenever a report leads to a conviction of a tax evader. The bounty to the informant is a proportion b, 0<b<1, of the total tax and fines collected from the tax evader. In addition informants may be motivated by a personal "revenge" motive. We assume, like Yaniv (2001), that each tax payer is coupled with a specific informant. (We use the term "informant" rather than the more accurate "potential informant".) This is based on the observation that informants are mostly disgruntled employees or jilted lovers or spouses. It may be argued that both informant's knowledge of the evasion, and his/hers negative feelings towards the tax payer are a result of their personal relationship.
We distinguish between the country's legistlation mechanisms and government, and the tax authority. We beleive that a tax authority would be typically restricted to follow the laws and implement policies decided by the former.
We assume that the tax authority may choose only pi and pr, and cannot influence β, b, π, and θ. We assume that the bounty rate b is decided within the country's legistlation mechanisms, and may consider the general issue of rewarding citizens who assist law enforcing authorities. Likewise, the fine rate π is decided within the country's legistlation mechanisms, which may take into account jutice principles concerning the adequet punishment for illegal activities. Also the tax rate θ is decided in a more general framework, that may take into account economic policy, government expenditure on public goods, tansfer payments policy, indirect taxes, etc.
The tax authority has a fixed budget B, B>0, for conducting tax audits. We assume it has several goals with the following priorities:
This means that first the tax authority chooses its policy variables to maximizes the total declared incomes, and if this problem has multiple solutions, it chooses among them those which maximize its taxation revenue.
Some models of taxation assume that the government maximizes the total taxes and fines collected minus costs. Our assumption takes into account that the tax authority is one of many government authorities, and as such it faces a budget consraint. The earnings from taxation are not added to the budget of the tax authority, but finance all the government's activities.
We believe that a democratic regime considers the citizens' law conformity as an important social goal. In the context of income tax, this may be measured by having the declared incomes as close as possible to the true ones. Maximizing the total declared incomes may be viewed as quantifying citizens' law conformity.
The cost function of auditing C, is only a function of the proportion of tax payers being audited, it is strictly increasing in this variable, and C[0]=0.
We make an additional assumption regarding the cost of auditing and the budget for auditing:
Assumption 1
C[Min{1/βπ,1}]>B where B>0 is the budget for auditing.
Assumption 1 guaranties that the tax authority cannot audit all tax payers, and that it cannot audit a high enough proportion, to make tax evasion not worthwhile.
We use the term "blowing the whistle" rather than reporting the tax payer to the tax authority. Once the tax payer declared his income, the informant chooses a probabilty q, 0≤q≤1 in which he blows the whistle. The informant's expected utility gain may be different from zero only if he blows the whistle. Thus whenever q>0. His utility gain involves direct monetary compensation from the tax authority, as well as non monetary gains due to the informant's "revenge motive".
When blowing the whistle, the informant suffers a cost K, K>0, that may be composed of both monetary and non-monetary components.
Denote by y, y≥0, the tax payer's true taxable income, and by x, 0≤x≤y, his declared income. βpibπθ(y-x) is the expected monetary compensation the informat receives once he blew the whistle.
In addition, once the tax payer is convicted, the informant gains a non-monetary utility of rπθ(y-x)+R, where r≥0 and R≥0 are utility parameters of the informat. The informant's non-monetary payoff is normalized to its monetary equivalent.
Therefore the informant's expected utility gain, assuming he is risk neutral, is:
EUG(q,y-x) = q[βpi((b+r)πθ(y-x)+R)-K].
The tax payer expected net income (ENI) is the sum of his net legitimate income (NLI) and the expected net evaded tax (ENET).
The tax payer's expected net income is therefore:
ENI(q,y,y-x) = NLI(y) + ENET(q,y-x), where NLI(y) = (1-θ)y, and ENET(q,y-x)= (y-x)θ(1-βπ(qpi+(1-q)pr)).
The players in the game are the tax payers, their associated informants, and the tax authority.
There is a continuum of tax payers, each of which is coupled with an informant. Every tax payer is negligble.
Formally, Let ⟨A,σ,μ⟩ be a measure space, where A=[0,1] is the set of tax payers-informant pairs, σ the collection of all measurable subsets of A, and μ is the Lesbegue measure on the unit interval. Let y:A⇒ℝ+ be the taxable incomes function. We assume that y is measurable.
We consider the following extensive form game:
Tax payer a∈A payoff is:
ENI(q(a),y(a),y(a)-x(a)) = NLI(y(a)) + ENET(q(a),y(a)-x(a)), where NLI(y(a)) = (1-θ)y(a), and ENET(q(a),y(a)-x(a))= (y(a)-x(a))θ(1-βπ(q(a)pi+(1-q(a))pr)).
Informant a∈A payoff is:
EUG(q(a),y(a)-x(a)) = q(a)[βpi((b+r)πθ(y(a)-x(a))+R)-K]
Within a subgame perfect equilibrium, h(a) denotes the history prior to the subgame in which pair a∈A moves. Let x(a,pi,pr,h(a)) be the tax payers' equilbrium strategies function. Namely, a function that assigns to each tax payer a, and taxation policy pair (pi,pr), and history h(a) the choice of declared income x. Likewise, let q(a,pi,pr,h(a),x(a)) be the informants' equilbrium strategies function.
Now we can state formally the tax authority primary goal. It is:
Max ∫x(a,pi,pr,h(a))dμ
s.t. C[pr(1-∫q(a,pi,pr,h(a),x(a))dμ) + pi∫q(a,pi,pr,h(a),x(a))dμ] ≤B
Where the maximum is chosen among all values of pr and pi satisfying
0≤pr≤pi,
and all the integrals above are taken over a∈A.
The tax authority expected net lost taxes (ENLT) is from a single tax payer:
ENLT(q,y-x)= (y-x)θ(1-βπ(qpi(1-b)+(1-q)pr)).
Note that ENLT differs from ENET due to the bounty payment to the informant.
The tax authority secondary goal is:
Min ∫ENLT(q(a,pi,pr,h(a),x(a)),y(a)-x(a,pi,pr),h(a))dμ
Where the minimum is taken over all taxation policy pairs (pi,pr) that solve the primary goal, and the integral is taken over a∈A.
From a game theoretic view the choice of the probabilities pi and pr cannot be restricted to by choices of other players. Thus, formally, the taxation authority has lexicographic preferences as discussed in the section "The taxation scenario."
...sub game perfect equiblirium vs sequential...
The eqilibrium is characterized by two critical evaded income levels, L and H.
In the regular case, 0<L<H. Whenever a tax payer under reports up to L dollars, the informant does not blow the whistle. A tax payer whose income is less than H under reports L dollars. If his income is less than L, he reports zero income. As the informant does not blow the whistle, the tax payer may be subject to a random audit.
If the tax payer's income is larger than H he chooses to declare zero income, the informant blows the whistle, and the tax payer may be subject to an audit due to the report. Depending on parameters' value, H may be infinite. Evidently, in this case, the tax payer cannot have an income larger than H.
We first analyse the informant's decision. Recall that his expected utility gain (EUG) is:
EUG(q,y-x) = q[βpi((b+r)πθ(y-x)+R)-K].
Observe that whenever βpi((b+r)πθ(y-x)+R)-K > 0 he will choose q=1. Analogously, whenever βpi((b+r)πθ(y-x)+R)-K < 0 he will choose q=0, and when βpi((b+r)πθ(y-x)+R)-K = 0 he is indifferent about the choice of q.
The critical value of y-x for which βpi((b+r)πθ(y-x)+R)-K = 0 is:
Definition 1
L(pi) = (K-βpiR)/βpi(b+r)πθ.
An increase in pi always reduces L.
To avoid the situation that the informant always blows the whistle, independetly of the evaded tax level, we assume:
Assumption 2 K-βR >0
As pi≤1, Assumption 2 guaranties that L(pi)>0.
To summarize:
Claim 1 An informant's strategy is a best response in every subgame if and only if it satisfies: q=1 when y-x>L(pi); q=0 when y-x<L(pi); and 0≤q≤1 when y-x=L(pi).
Proof: See the above disscussion.
The following definition is useful in many of the proofs:
Definition 2
The
If follows directly from Claim 1, that the informant's reference strategy, is a best response in every sub game.
We now turn to study the tax payer's decision. Recall that his expected net income is:
ENI(q,y,y-x) = NLI(y) + ENET(q,y-x) = (1-θ)y + (y-x)θ(1-βπ(qpi+(1-q)pr))
As NLI(y) is exogenous to the tax payer's decision, we may concentrate on maximizing ENET(q,y-x).
We will now look for an income level H that has the following property: When a tax payer has a taxable income larger than H he would prefer to declare zero and be reported to the tax authority by the informant, rather than just evading L, and be potentially subject to a random audit.
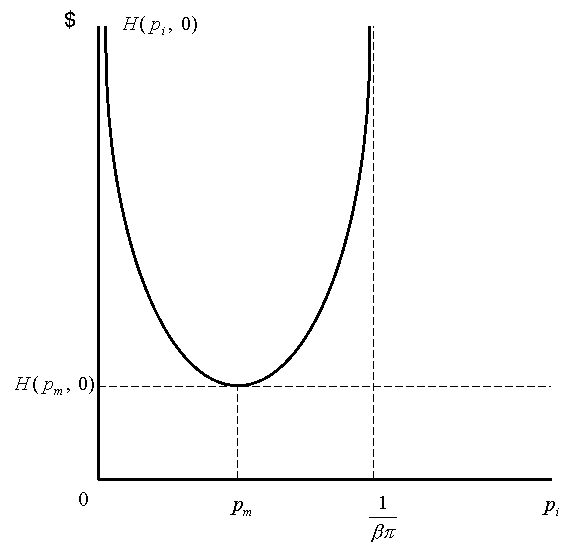
Assumption 1 implies that pr<1/βπ. Therefore, we distinguish between three possibilities. In the first pr<pi<1/βπ, in the second pr<1/βπ≤pi, and in the third pr=pi<1/βπ.
In the first possibility, ENET is inceasing in y-x also when q=1. We define H(pi,pr) as the evaded income level that solves the equation:
ENET(0,L) = ENET(1,H).
It may be easily shown that:
H(pi,pr) =
(K-βpiR)(1-πβpr)/βpi(b+r)πθ(1-πβpi)
As pr<pi we have that H(pi,pr)>L(pi).
In the second possibility, pi≥1/βπ. Hence we define H(pi,pr)=∞, as ENET(0,L)>ENET(1,y-x) for all choices of y-x, and the tax payer always prefers to evade at most L and not to be reported.
In the third possibility pr=pi we define H(pi,pr)=0, as in this irregular case, the tax payer is indifferent between being reported or not.
To summarize we have:
Definition 3
| H(pi,pr) = | { | 0, | if pi=pr<1/βπ |
| (K-βpiR)(1-πβpr)/βpi(b+r)πθ(1-πβpi), | if pr<pi<1/βπ | ||
| ∞, | if pr<1/βπ≤pi |
An increase in pi may increase or decrease H. It may be shown, however, that when pi>1/2π an increase in pi will increase H.


Proposition 1
In a subgame perfect equilibrium,
1. If y<L(pi)<H(pi,pr)
The tax payer chooses x=0, and the informant does not blow the whistle.
2. If L(pi)≤y<H(pi,pr), the tax payer chooses x=y-L(pi), and the informant does not blow the whistle.
3. If L(pi)<y=H(pi,pr)
the tax payer chooses x=H(pi,pr)-L(pi), and the informant does not blow the whistle, or x=0 and the informant blows the whistle.
4. If L(pi)<H(pi,pr)<y, the tax payer chooses x=0 and the informant blows the whistle.
5. If H(pi,pr)=0, the tax payer chooses x=0.
Proof:
1. First consider the strategy pair in which the tax payer chooses x=0, and the informant chooses his reference strategy. As already noted, it follows from Claim 1, that the informant's strategy is a best reponse in every subgame. Also as ENET(0,y-x) is strictly increasing in y-x, choosing x=0 is a best response. Therefore the above mentioned strategy pair is a subgame perfect equilibrium.To see that there are no other equilibrium outcomes, note that it follows from Claim 1, that for any value of y-x<L(pi); the only best response of the informant is q=0. Given that, the tax payer's choice x=0 is the only best response, hence no other equilbrium outcome may prevail
2. Consider the strategy pair in which the tax payer chooses y-x=L(pi), and the informant chooses his reference strategy. As already noted, it follows from Claim 1, that the informant's strategy is a best reponse in every subgame. By the consrtuction of H(pi,pr), it follows that ENET(0,L(pi))<ENET(1,y-x) whenever y-x<H(pi,pr). Hence also the tax payer's strategy is best response.
To see that there is no other equilibrium outcome, note that the tax payer may assure himself a payoff as close as he wants to ENET(0,L(pi)) by choosing y-x slightly smaller than L(pi). Therefore, the tax payer's payoff cannot be smaller than ENET(0,L(pi)). However the only way to achieve this payoff is by the tax payer choosing y-x=L(pi), and the informant choosing q=0 in response.
3. Consider two strategy pairs in the first, the tax payer chooses x=H(pi,pr)-L(pi), and the informant chooses his reference strategy, and in the second the tax payer chooses x=0, and the informant chooses his reference strategy. As already noted, it follows from Claim 1, that the informant's strategy is a best reponse in every subgame. By the consrtuction of H(pi,pr), it follows that ENET(0,L)=ENET(1,H). Hence in both strtegy pairs the tax payer's strategy is a best response.
To see that there are no other equilbrium outcomes note that it follows from claim 1, that the tax payer's maximum payoff is ENET(1,H). The only two possible ways to achieve this payoff are those sugested in the proposition.
4. Consider the strategy pair in which the tax payer chooses x=0, and the informant chooses his reference strategy. As already noted, it follows from Claim 1, that the informant's strategy is a best reponse in every subgame. By the consrtuction of H(pi,pr), it follows that ENET(0,L)<ENET(1,y), whenever y>H. Hence the tax payer's strategy is a best response.
To see that there are no other equilbrium outcomes note that it follows from claim 1, that the tax payer's maximum payoff is ENET(1,y). The only possible way to achieve this payoff is the one sugested in the proposition.
5. Consider the strategy pair in which the tax payer chooses x=0, and the informant chooses his reference strategy. As already noted, it follows from Claim 1, that the informant's strategy is a best reponse in every subgame. As pi≤pr, it follows that ENET(0,y)<ENET(1,y), for all y. Hence the tax payer's strategy is a best response.
To see that there are no other equilbrium outcomes note that it follows from claim 1, that the tax payer's maximum payoff is ENET(1,y). The only possible way to achieve this payoff is the one sugested in the proposition.
Let F be the commulative disribution function of the gross individual incomes. Namely F(z)=μ({a∈A:y(a)≤z}). As any commulative distribution function, F is non-decresing, continuous from the right, and satisfies: 0≤F(z)≤1, for all z. F(∞)=1. As y(a)≥0 for all tax payers, we also have: F(z)=0, for all z<0
Our analysis earlier in the article predicts that the income reported x is a (deterministic) function of y, with one exception. When y=H(pi,pr), x may take two different values. We will show later, that within our assumptions on the distribution of incomes, all subgame perfect equilibria in the game where the tax authority is a player, x=H(pi,pr)-L(pi) if y=H(pi,pr) whenever there is a positive measure of tax payers with this taxable income.
Hence the tax authority primary goal is:
Max ∫{y: L≤y≤H}(y-L)dF
s.t. C[prF(H) + pi(1-F(H))] ≤ B
Where the maximum is chosen among all feasible values of (pr,pi)
The tax authority secondary goal is:
Min
∫{y:0≤y<L}ENLT(0,y)dF +
∫{y:L≤y≤H}ENLT(0,y-L)dF +
∫{y:H<y}ENLT(1,y)dF
Where the minmum is taken over all pairs of
(pr,pi) that solve the primary goal.
We shall disscuss in the following sub sections three different distribution families of taxable incomes. The first two are descrete distriburtions common in the tax evasion literature. In the first all tax payers have an identical taxable income, and in the second there are two levels of taxable incomes.
Distribution Family 1 All tax payers have an identical taxable income y1, 0<y1, y1≠H(1,0), y1≠L(1).
Distribution Family 2 There are two levels of taxable incomes y1 and y2, 0<y1<y2, y1≠H(1,0), y1≠L(1),y2≠H(1,0), y2≠L(1) and F(y1)=α.
The third family is of continuous distributions.
Distribution Family 3 F is continuous and 0<F(z)<∞ for all z>0.
Theorem 1
Consider the case where all tax payers earn an identical income y1.
| F(y) = | { | 0, | if y<y1 |
| 1, | if y1≤y |
Definition 4
The tax payer's reference strategy is declaring x=Max{0,y-L(pi)} whenever y≤H(pi,pr) and choosing x=0 whenever y>H(pi,pr).
Proof of Theorem 1:
First, we show that there are equilibria with the properties stated in the theorem.
Consider equilibria in which the informants and tax payers play according to their reference strategies (see Definitions 2 and 4). It follows from Proposition 1, that these starategies are consistent with subgame perfect equilibrium. The tax authority, given the informants and tax payers equilibrium strategies, will maximize the total declared incomes within the budget constraint, and within the solutions to this optimization problem, will minimize ENLT. In order to achieve its goals the taxation authiority should keep y1≤H and minimize L within this constraint. If this problem has more than one solution, the taxation authority will choose those that minimize ENLT.
Now we show that there are no other equilibrium outcomes.
In all cases where in the above equilibria the tax authority chose policies that lead to y1=H, it could guarantee achieving values of its primary or secondary goals as close as possible to those in the suggested equilibria by making y1<H. This implies that the taxation authority does achieve the exact values suggested in any subgame perfect equilibrium.
Theorem 2
Consider the case where there are two levels of income. Some tax payers earn y1, and some earn y2, y1<y2.
| F(y) = | { | 0, | if y<y1 |
| α, | if y1≤y<y2; | ||
| 1, | if y2≤y |
Case 3.1: pi*=pi**
(1) pi=pi*, pr=0
(2) The lower income tax payers declare x=Max{0,y1-L(pi*)} and their corresponding informants do not blow the whistles.
(3) The higher income tax payers declare x=y2-L(pi*) and their corresponding informants do not blow the whistles.
Case 3.2: pi*≠pi** and
αMax{y1-L(pi*),0}+(1-α)(y2-L(pi*)>α(y1-L(pi**))
(1) pi=pi*, pr=0
(2) The lower income tax payers declare x=Max{0,y1-L(pi*)} and their corresponding informants do not blow the whistles.
(3) The higher income tax payers declare x=y2-L(pi*) and their corresponding informants do not blow the whistles.
Case 3.3: pi*≠pi** and
αMax{y1-L(pi*),0}+(1-α)(y2-L(pi*)<α(y1-L(pi**))
(1) pi=pi**, pr=0
(2) The lower income tax payers declare x=y1-L(pi**) and their corresponding informants do not blow the whistles.
(3) The higher income tax payers declare x=0 and their corresponding informants blow the whistles.
Case 3.4: pi*≠pi** and
αMax{y1-L(pi*),0}+(1-α)(y2-L(pi*)=α(y1-L(pi**))
The equilibrium outcomes will be like in 3.3.
Proof:
The proof is similar to that of Theorem 1. In the first two cases, i.e. where y1<L(1), or where L(1)<y1<y2<H(1,0), the proof is essentially identical to that of Theorem 1.
In the last case, where L(1)<y1 and H(1,0)<y2, the tax authority considers two alternatives. In the first one H is larger or equal the highest income. In the second alternative y2<H, so the higher income tax payers declare no income, but as pi is higher, L is lower and the lower income tax payers declare a larger part of their incomes compared to the first alternative.
In case 3.1 the second alternative is irrelevant. In case 3.2 the first alternative gives the tax authority better results, and in case 3.3 the second alternative is preferable. Case 3.4 represents the case where both alternatives give an identical result per the primary goal. Hence the second alternative is chosen, as it gives better results per the secondary goal.